Single particle
The momentum of a particle is traditionally represented by the letter
p. It is the product of two quantities, the
mass (represented by the letter
m) and
velocity (
v):
[1]
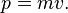
The units of momentum are the product of the units of mass and velocity. In
SI units,
if the mass is in kilograms and the velocity in meters per second, then
the momentum is in kilograms meters/second (kg m/s). Being a vector,
momentum has magnitude and direction. For example, a model airplane of
1 kg, traveling due north at 1 m/s in straight and level flight, has a
momentum of 1 kg m/s due north measured from the ground.
Many particles
The momentum of a system of particles is the sum of their momenta. If two particles have masses
m1 and
m2, and velocities
v1 and
v2, the total momentum is

The momenta of more than two particles can be added in the same way.
A system of particles has a
center of mass, a point determined by the weighted sum of their positions:
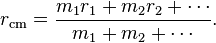
If all the particles are moving, the center of mass will generally be
moving as well. If the center of mass is moving at velocity
vcm, the momentum is:

This is known as
Euler's first law.
[2][3]
Relation to force
If a force
F is applied to a particle for a time interval
Δt, the momentum of the particle changes by an amount

In differential form, this gives
Newton's second law: the rate of change of the momentum of a particle is equal to the force
F acting on it:
[1]
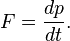
If the force depends on time, the change in momentum (or
impulse) between times
t1 and
t2 is

The second law only applies to a particle that does not exchange matter with its surroundings,
[4] and so it is equivalent to write

so the force is equal to mass times
acceleration.
[1]
Example: a model airplane of 1 kg accelerates from rest to a
velocity of 1 m/s due north in 1 s. The thrust required to produce this
acceleration is 1
newton. The change in momentum is 1 kg m/s.
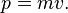

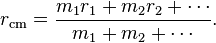


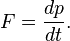


Tidak ada komentar:
Posting Komentar