Relativistic mechanics
Lorentz invariance
Newtonian physics assumes that absolute time and space exist outside of any observer; this gives rise to the Galilean invariance described earlier. It also results in a prediction that the speed of light can vary from one reference frame to another. This is contrary to observation. In the special theory of relativity, Einstein keeps the postulate that the equations of motion do not depend on the reference frame, but assumes that the speed of light c is invariant. As a result, position and time in two reference frames are related by the Lorentz transformation instead of the Galilean transformation.[25]Consider, for example, a reference frame moving relative to another at velocity v in the x direction. The Galilean transformation gives the coordinates of the moving frame as
The modified momentum,
Four-vector formulation
Main article: Four-momentum
In the theory of relativity, physical quantities are expressed in terms of four-vectors
that include time as a fourth coordinate along with the three space
coordinates. These vectors are generally represented by capital letters,
for example R for position. The expression for the four-momentum
depends on how the coordinates are expressed. Time may be given in its
normal units or multiplied by the speed of light so that all the
components of the four-vector have dimensions of length. If the latter
scaling is used, an interval of proper time, τ, defined by[28]The magnitude of the momentum four-vector is equal to m0c:
The relativistic energy–momentum relationship holds even for massless particles such as photons; by setting m0 = 0 it follows that
Classical electromagnetism
In Newtonian mechanics, the law of conservation of momentum can be derived from the law of action and reaction, which states that the forces between two particles are equal and opposite. Electromagnetic forces violate this law. Under some circumstances one moving charged particle can exert a force on another without any return force.[31] Moreover, Maxwell's equations, the foundation of classical electrodynamics, are Lorentz-invariant. However, momentum is still conserved.Vacuum
In Maxwell's equations, the forces between particles are mediated by electric and magnetic fields. The electromagnetic force (Lorentz force) on a particle with charge q due to a combination of electric field E and magnetic field (as given by the "B-field" B) isIn a vacuum, the momentum per unit volume is
Media
The above results are for the microscopic Maxwell equations, applicable to electromagnetic forces in a vacuum (or on a very small scale in media). It is more difficult to define momentum density in media because the division into electromagnetic and mechanical is arbitrary. The definition of electromagnetic momentum density is modified toParticle in field
If a charged particle q moves in an electromagnetic field, its kinematic momentum m v is not conserved. However, it has a canonical momentum that is conserved.Lagrangian and Hamiltonian formulation
The kinetic momentum p is different to the canonical momentum P (synonymous with the generalized momentum) conjugate to the ordinary position coordinates r, because P includes a contribution from the electric potential φ(r, t) and vector potential A(r, t):[21]Classical mechanics Relativistic mechanics Lagrangian 

Canonical momentum 
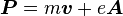
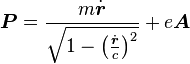
Kinetic momentum 
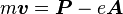

Hamiltonian 

The classical Hamiltonian
 for a particle in any field equals the total energy of the system - the kinetic energy T = p2/2m (where p2 = p·p, see dot product) plus the potential energy V. For a particle in an electromagnetic field, the potential energy is V = eφ, and since the kinetic energy T always corresponds to the kinetic momentum p, replacing the kinetic momentum by the above equation (p = P − e''A) leads to the Hamiltonian in the table.
for a particle in any field equals the total energy of the system - the kinetic energy T = p2/2m (where p2 = p·p, see dot product) plus the potential energy V. For a particle in an electromagnetic field, the potential energy is V = eφ, and since the kinetic energy T always corresponds to the kinetic momentum p, replacing the kinetic momentum by the above equation (p = P − e''A) leads to the Hamiltonian in the table.These Lagrangian and Hamiltonian expressons can derive the Lorentz force.
Canonical commutation relations
The kinetic momentum (p above) satisfies the commutation relation:[21]Quantum mechanics
Further information: Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle
defines limits on how accurately the momentum and position of a single
observable system can be known at once. In quantum mechanics, position
and momentum are conjugate variables.For a single particle described in the position basis the momentum operator can be written as
For both massive and massless objects, relativistic momentum is related to the de Broglie wavelength λ by


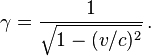





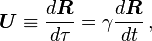
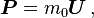
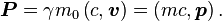
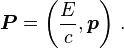

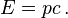






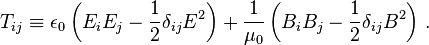
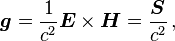

![\left [ p_j , p_k \right ] = \frac{i\hbar e}{c} \epsilon_{jk\ell } B_\ell](http://upload.wikimedia.org/math/9/8/9/989828171b1314ed1121c3a586b12041.png)
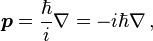
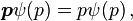

Tidak ada komentar:
Posting Komentar